RSA, Blind Signatures, and a VolgaCTF Crypto Challenge

March 31, 2019

Categories: cryptography, security

Word count: 2304

Maple Bacon participated in VolgaCTF 2019, which ran for 48 hours from March 29th at 15:00 UTC. We were all pretty busy, with it being the last week of classes, but we managed to finished 41st out of 1097 teams. In addition to the challenge in this writeup, I also solved Store (Web 100), Fakegram Star (Antifake 75), and Horrible Retelling (Antifake 50).

I wrote this since it was my first time looking in depth at a crypto problem. I researched and tried to understand how the RSA encryption algorithm worked (including all the math - keep reading for an actual proof), as well as the blinding and unblinding functions, and incorporated these into my exploit.

Understanding the Problem
Diving into RSA
RSA Signatures
Blinding and Unblinding Functions
The Exploit

Blind - Crypto 200

Description

Pull the flag...if you can.

nc blind.g.2019.volgactf.ru 7070

server.py

Understanding the Problem

I like to connect to the box to take a look at what happens and the input/outputs that we're looking at. Using netcat, we connect to the port and see this:

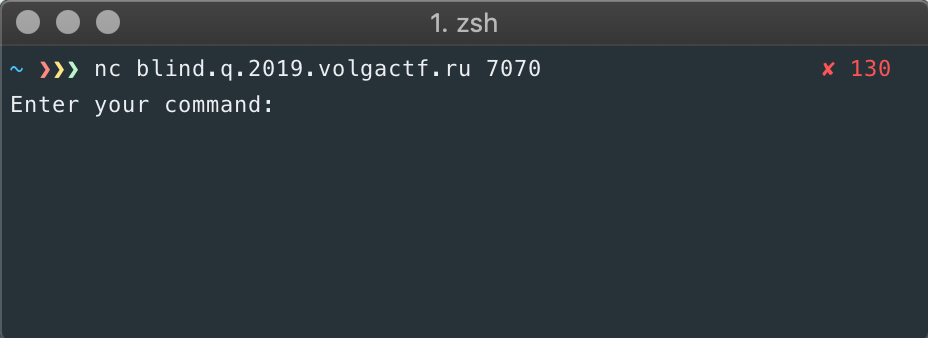
Looks like it's asking for a command. Perhaps a Linux command might work?

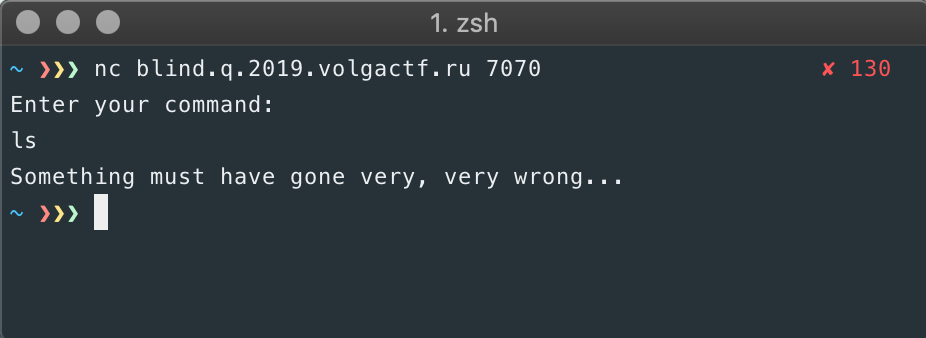
That didn't work. Guess that might have been too easy. Let's take a look at the server.py file that was helpfully provided for us. Let's skip down to the main function and try to figure out what the server's doing.

if __name__ == '__main__':
    signature = RSA(e, d, n)
    check_cmd_signatures(signature)
    try:
        while True:
            send_message('Enter your command:')
            message = read_message().strip()
            (sgn, cmd_exp) = message.split(' ', 1)

There are a couple points of interest here:

signature is initialized to an object of the RSA class, with the variable e, d, and n. Looking through the script, we see that n and e are local variables in the section nicely commented as Keys. However, d is imported in from another Python module, private_key in the line from private_key import d.
check_cmd_signatures(signature) just seems to do a verification that the signing process is working properly, so we can ignore that.
We see the message that we get when we connect to the box: "Enter your command". When we put an input, read_message().strip() removes the whitespace. More importantly, the next line tells us that the expression is split into sgn and cmd_exp.

That last point is pretty significant. When we scroll down to the bottom, we see that one of the catch statements is:

except Exception as ex:
    send_message('Something must have gone very, very wrong...')
    eprint(str(ex))

Since our input was only a single word, it wasn't able to unpack the message into the two separate variables and threw an Exception.

After the input is unpacked, the server uses shlex to get an array of the command in a shell-like syntax.

cmd_l = shlex.split(cmd_exp)
cmd = cmd_l[0]

shlex.split is similar to split() but instead of splitting on a delimiter, also respects quotes. For example, shlex.split("cd 'my folder'") will give you ["cd", "'my folder'"] while "cd 'my folder'".split() gives you ['cd', "'my", "folder'"].

We'll have to keep this in mind when writing our exploit, since the nuisances with the quotes may cause problems.

Skimming through the rest of the function, we see that it's designed to work with commands that start with ls, dir, cd, cat, sign, exit, or leave. Any other command will cause the script to exit with "Unknown command".

If we look at the if statement for ls and dir, we see:

if cmd == 'ls' or cmd == 'dir':
    ret_str = run_cmd(cmd_exp)
    send_message(ret_str)

This seems to say that these commands aren't verified and will just run on the server. Let's just give this a shot. I use 1 ls because we know that the script splits the command into two parts, and the second part is used as the cmd in the if statements. We don't know anything about the sgn right now, so we'll just put something random for now, which works because the script won't do anything with it if the command is ls.

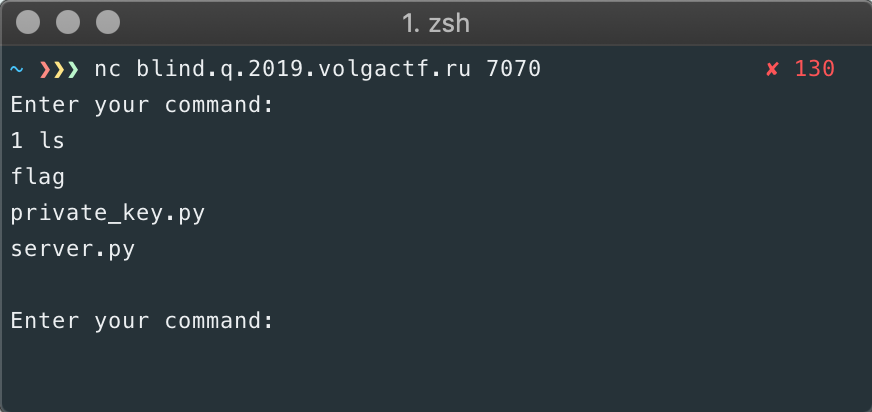
Nice! Looks like the private_key.py file I mentioned earlier is there, along with the flag file that we'll probably want to read. Can we run cat flag to just easily grab it?

😞

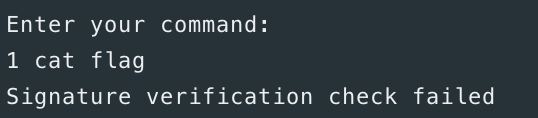
So the server doesn't just let us run any command we want. Let's go back to the script and try to figure out how it does this signature verification check.

elif cmd == 'cat':
    try:
        sgn = int(sgn)
        if not signature.verify(cmd_exp, sgn):
            raise SignatureException('Signature verification check failed')
        if len(cmd_l) == 1:
            raise Exception('Nothing to cat')
        ret_str = run_cmd(cmd_exp)
        send_message(ret_str)
    except Exception as ex:
        send_message(str(ex))

sgn is converted into an integer, and then sent to signature.verify, along with the command. If it passes that check, the server will run our command, so we have to find a way for our command to verify successfully.

How do commands get signed? Let's take a look at the script for the sign command.

elif cmd == 'sign':
    try:
        send_message('Enter your command to sign:')
        message = read_message().strip()
        message = message.decode('base64')
        cmd_l = shlex.split(message)
        sign_cmd = cmd_l[0]
        if sign_cmd not in ['cat', 'cd']:
            sgn = signature.sign(sign_cmd)
            send_message(str(sgn))
        else:
            send_message('Invalid command')
    except Exception as ex:
        send_message(str(ex))

In short, this command will sign any message encoded in base64 except for the ones that start with cat or cd. Looks like they really don't want us reading any of the other files on the server.

The signature can be analyzed in the RSA class.

class RSA:
    def __init__(self, e, d, n):
        self.e = e
        self.d = d
        self.n = n

    def sign(self, message):
        message = int(message.encode('hex'), 16)
        return pow(message, self.d, self.n)

    def verify(self, message, signature):
        message = int(message.encode('hex'), 16)
        verify = pow(signature, self.e, self.n)
        return message == verify

I had no idea what RSA cryptography was when I started looking into this challenge, so I started researching some background information on how it works.

Diving into RSA

RSA (Rivest-Shamir-Adleman) is an asymmetric encryption algorithm, which uses prime factorization as the trapdoor function.

The trapdoor function refers to a very important concept in cryptography: it is trivial to go from one state to another, but going the opposite direction, without specific information, becomes unfeasible. In other words, the function is one-way. You can imagine this being extremely useful, since you want to be able to quickly encrypt a message, but make it difficult for just anyone to decrypt it.

Prime factorization (or integer factorization) is a number theory concept that every positive integer can be broken down into composite prime numbers. The prime factorization of extremely large numbers cannot be efficiently computed, and the hardest instances are semiprimes, which is when the number is the product of two primes. If the two primes are close enough, they can be factored using Fermat's method, but if they aren't close enough together, trial and error can be more efficient than Fermat's – which, suffice to say, isn't efficient at all. Computing the prime factors of a very large number is known as the RSA problem.

RSA Encryption and Decryption

The RSA algorithm works with the following four steps:

1. Key Generation

Two large prime numbers, p and q, are picked. These should be similar in magnitude, but differ in length so Fermat's method will not work.
You use these numbers to compute
$n = pq \tag{RSA:1}$
n will be the modulus for both the public and the private keys. Its length is usually expressed in bits and is known as the key length. n will be made public.
Compute the Euler totient function:
$\phi(n) = (p-1)(q-1) \tag{RSA:2}$
Carmichael's totient function λ(n) can also be used, since φ(n) is always divisible by λ(n).
$\lambda(n) = lcm(p-1, q-1) \tag{RSA:3}$
Select e such that it is between 3 and n-1 that is relatively prime to p-1 and q-1. Relatively prime, or coprime, means that the only common factor between them is 1, or that it's greatest common denominator is 1. Equivalently:
$gcd(e, \phi(n)) = 1$ or $gcd(e, \lambda(n)) = 1 \tag{RSA:4}$
Compute d as the multiplicative inverse of e modulo λ(n) as
$d = e^{-1} \text{ mod } \phi(n)$ or $d = e^{-1} \text{ mod } \lambda(n) \tag{RSA:5}$

The public key will consist of modulus n and public exponent e. The private key will consist of the private exponent d.

2. Key Distribution

Let's say Bob wants to send Alice his message M. Bob needs Alice's public key to encrypt the message, and Alice uses her private key to decrypt the message.

Alice sends Bob her public key (n, e) to Bob, while keeping the private key secret.

3. Encryption

To encrypt message M, first turn the message into an integer m, such that 0 ≤ m < n, with a reversible padding scheme known by both parties. This turns the message into a numeric form for encryption.

The ciphertext C is computed by raising m to the eth power modulo n.

C \equiv E(M) \equiv m^e \text{ mod } n \tag{RSA:6}

4. Decryption

You can recover message m by using the private key d. Compute:

m \equiv D(C) \equiv C^d \text{ mod } n \tag{RSA:7}

Given m, you can easily compute M by reversing the padding scheme.

For a proof of correctness of this encryption and decryption algorithms, section VI The Underlying Mathematics of the original RSA paper is a very interesting read.

RSA Signatures

Phew. That was quite a lot of information. But that still doesn't explain how our challenge is going to be solved. The server implements RSA signing.

When you are encrypting a message, you use the recipient's public key, and they decrypt it with their private key.
When signing a message, you use your private key, and the recipient verifies that the message is yours using your public key.

What the server is doing when signing is using their private key d to essentially encrypt the input with the private key, which we can verify by looking at the function in the server script (yes, we're still working on this challenge):

def sign(self, message):
    message = int(message.encode('hex'), 16)
    return pow(message, self.d, self.n)

So the message is M is transformed into integer m by encoding it to hex, then returned by raising it to the dth power mod n. This gives you the signed message, which is signature S. Mathematically:

S \equiv m^d \text{ mod } n

To verify the signature, it computes the inverse of this in the verify function.

def verify(self, message, signature):
    message = int(message.encode('hex'), 16)
    verify = pow(signature, self.e, self.n)
    return message == verify

Which gives you

m' \equiv S^e \text{ mod } n

If m' = m, then you can verify that the signature is correct. The verify function compares your message (the command cat flag in our case) with the signed version of it, and will return true if it matches.

However, our server refuses to sign cat flag. How can we trick the server into signing it? I actually spent a long time trying to figure this out – I actually tried to factor p and q from n at the start before I knew any better. Just when I was about to give up and click on another challenge, I realized that the challenge was named Blind. Why? That led me to my next search.

Blind Signatures

Many times, for privacy and anonymity, you want to be able to have a message signed without the signer knowing what the message is – for example, in electronic voting or digital currency. This is called a blind signature.

Let's say Bob wants Alice to sign a message, but he doesn't want her to read it. These steps are followed to obtain Alice's signature:

Bob "blinds" the message m with a random number b, which is known as the blinding factor. Let's call this blind(m, b).
Alice signs the message, so we get signed(blind(m, b), d). This is signed with her private key d, so Bob does not know this.
Bob "unblinds" the message with b, getting unblinded(signed(blind(m, b), d), b). The blind and unblind functions must reduce to signed(m, d), which is Alice's signature on m.

That sounds like exactly what we want. Let's analyze our problem:

We want the server to sign cat flag.
The server refuses to sign any message starting with cat.
But the server will sign any other message. If we blind cat flag, send it to the server to sign the blinded message (which it doesn't know is one of the blacklisted commands), and then unblind it, we will be able to get its signature on our command.

Let's go about building the exploit.

Blinding and Unblinding Functions

These are going to work like this.

For a message M, convert it to an integer equivalent m. We will also choose a random value k, which can be any integer that is coprime to n. k^e mod n will be the blinding factor. Given e as the public exponent and n as the modulus, same as in the RSA signing process, we will blind the message m by multiplying it with the blinding factor as follows:

m' \equiv mk^e \text{ mod } n \tag{Blind:1}

We get the blinded message m'. We will send m' to be signed, and it will return as:

S' \equiv (m')^d \text{ mod } n \tag{Blind:2}

where S' is the signed blinded message. Because the message doesn't start with cat or any other blacklisted command, the server will happily do this for us. Now, the unblinded signature can be calculated by dividing by k.

S = \frac{S'}{k} \text{ mod } n \tag{Blind:3}

Proof

More mathy stuff but I found it interesting so wanted to write it here. Let's prove that this actually works. The verify function will raise the signed message S to the eth power, and compare this with the original message m to check that they are equal. The verification can be written as so, and we can substitute in (Blind:2):

S^e \equiv (\frac{S'}{k})^e \text{ mod } n \equiv \frac{(S')^e}{k^e} \text{ mod } n \tag{Blind:4}

With (Blind:2), we can substitute S':

S^e \equiv \frac{(m')^{ed}}{k^e} \text{ mod } n \tag{Blind:5}

Because RSA keys satisfy the equation:

k^{ed} \equiv k \text{ mod } n

We can reduce (Blind:5) further.

S^e \equiv \frac{(m')}{k^e} \text{ mod } n \tag{Blind:6}

Substituting (Blind:1) into (Blind:6), we get:

S^e \equiv \frac{mk^e}{k^e} \equiv m \text{ mod } n \tag{Blind:7}

This demonstrates that the unblinded signature is passed in through the verify function, it will prove to be equal to the original message m.

The Exploit

If you've skipped all the way down here, here's the lowdown:

We need to build the function blind, which will multiply your command by the blinding factor k^e mod n.
We need to build the function unblind, which will divide by k mod n.
We send the blind(m) to the server, which will sign it. We take the response and unblind it, giving us the signature on the original command.
We then send the signature and the original command to the server, which will successfully pass the verification and run the command.

Blind

def blind(message):
    message = int(message.encode('hex'), 16) # original message in hex
    message = message * pow(k, e, n) # blinded message in hex
    message = long_to_bytes(message) # back to string
    message = "'" + message + "'"  # to get around shlex.split
    message = base64.b64encode(message) # input to sign must be base64 encoded
    return message

As mentioned earlier, since the server uses shlex.split, we need to put single quotes around the command for it to be parsed properly. Comments inline explaining what I'm doing should be pretty straightforward.

Unblind

def unblind(blinded_sgn):
    # unblind by m / (k % n)
    return str(int(blinded_sgn, 10) * inverse(k, n))

I originally had int(blinded_sgn, 10) / (k % n), but Python's division operator is an integer divide, not a modular divide. Equivalently, we can multiply by the inverse mod of k and n instead, which is from PyCrypto. (Shoutout to our amazing coach Robert for helping me with this!)

Script

Here's the full script that connects to the server and spits out the flag.

import binascii
from pwn import *
from Crypto.Util.number import inverse, long_to_bytes
import base64

n = 26507591511689883990023896389022361811173033984051016489514421457013639621509962613332324662222154683066173937658495362448733162728817642341239457485221865493926211958117034923747221236176204216845182311004742474549095130306550623190917480615151093941494688906907516349433681015204941620716162038586590895058816430264415335805881575305773073358135217732591500750773744464142282514963376379623449776844046465746330691788777566563856886778143019387464133144867446731438967247646981498812182658347753229511846953659235528803754112114516623201792727787856347729085966824435377279429992530935232902223909659507613583396967
e = 65537
k = 5 # change this if you get "no closing quotation"

def blind(message):
    # blinds the message by multiplying by k^e mod n
    message = int(message.encode('hex'), 16) # original message in hex
    message = message * pow(k, e, n) # blinded message in hex
    message = long_to_bytes(message) # back to string
    message = "'" + message + "'"  # to get around shlex.split
    message = base64.b64encode(message)
    return message

def unblind(blinded_sgn):
    # unblind by m / (k % n)
    return str(int(blinded_sgn, 10) * inverse(k, n))

msg = "cat flag"
r = remote("blind.q.2019.volgactf.ru", 7070)
r.recvuntil("Enter your command:")
r.send("1 sign\n")
r.recvuntil("Enter your command to sign:")
blinded_msg = blind(msg)
r.send(blinded_msg + "\n")
signed_blinded = r.recvuntil("Enter").strip("Enter")
print("signed blinded: " + signed_blinded)
r.close()

signature = unblind(signed_blinded)
print("unblinded signature: " + signature)

r = remote("blind.q.2019.volgactf.ru", 7070)
r.recvuntil("Enter your command:")
r.send(signature + " " + msg + "\n")
a = r.recvuntil("Enter").strip("Enter")
print(a) # flag should print here!
r.close()

Sometimes, if you're unlucky, your randomly blinded message contains ', and the server's shlex.split will get confused; you'll get the error "No closing quotation". If this happens, just change the k value until it works.

You can also send the message cat private_key.py to see the value of d that the server is using the sign the commands as well for funsies.

We finally get the flag: VolgaCTF{B1ind_y0ur_tru3_int3nti0n5} ★